백준 11048번 이동하기 C++

출처 : https://www.acmicpc.net/problem/11048

 

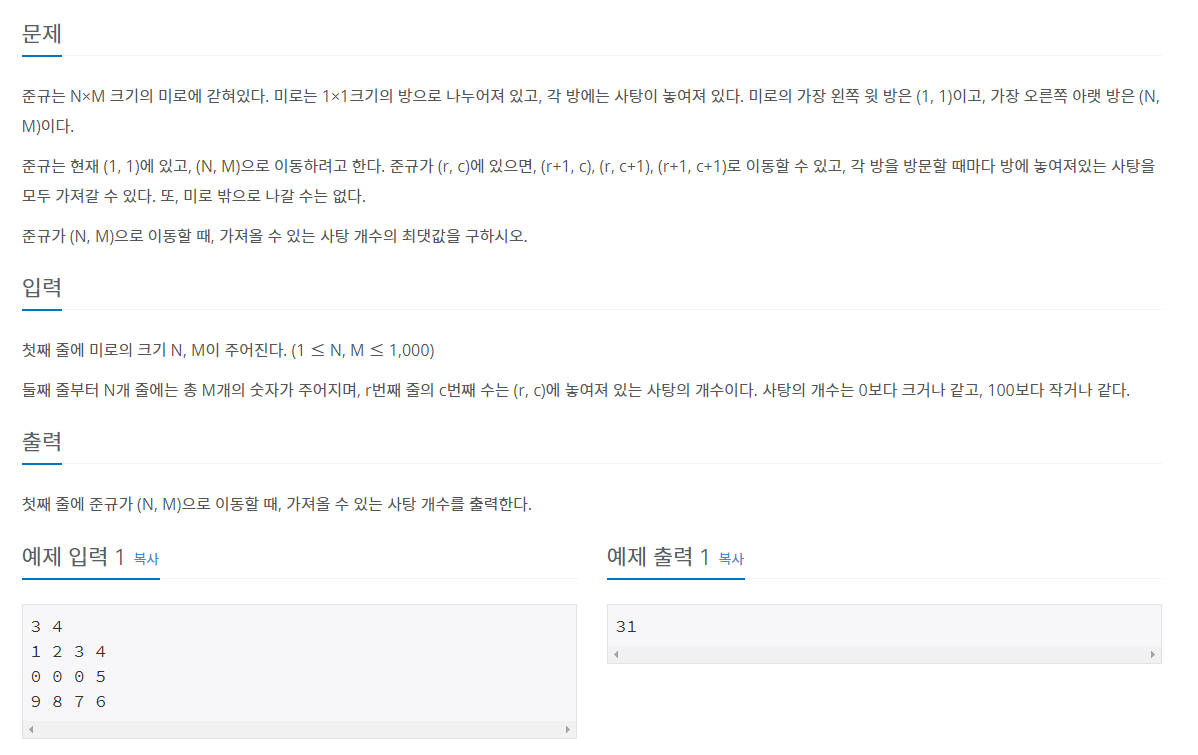
간단한 dp 문제이다.

(r, c)에서의 사탕의 최대값은 (r - 1, c) , (r, c - 1), (r - 1, c - 1) 중 누적된 사탕의 개수가 가장 큰 값에 현재 위치의 사탕의 수를 더하면 된다.

여기서 만들 수 있는 점화식은 dp[i][j] = max(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + v[i][j] 이다.

 

#include <iostream>
#include <string>
#include <vector>
#include <math.h>
#include <algorithm>
#include <utility>
#include <stack>
#include <queue>
#include <math.h>
#include <set>
#include <unordered_set>

using namespace std;
typedef long long ll;

int main() {
	ios_base::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int n, m;
	cin >> n >> m;
	vector<vector<int>> v(n + 1, vector<int>(m + 1, 0));
	vector<vector<int>> dp(n + 1, vector<int>(m + 1, 0));
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			cin >> v[i][j];
		}
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			dp[i][j] = max(dp[i - 1][j - 1], max(dp[i - 1][j], dp[i][j - 1])) + v[i][j];
		}
	}
	cout << dp[n][m];
};